Exact significance test (with respect to a single feature) for hierarchical clustering

This tests the null hypothesis of no difference in means in the mean of feature feat between clusters k1 and k2 at level K in a hierarchical clustering. (The K clusters are numbered as per the results of the cutree function in the stats package.)

test_hier_clusters_exact_1f(
  X,
  link,
  hcl,
  K,
  k1,
  k2,
  feat,
  indpt = TRUE,
  sig = NULL,
  covMat = NULL
)

Arguments

X

\(n\) by \(p\) matrix containing numeric data.

link

String selecting the linkage. Supported options are "single", "average", "centroid", "ward.D", "median", and "mcquitty".

hcl

Object of the type hclust containing the hierarchical clustering of X.

K

Integer selecting the total number of clusters.

k1, k2

Integers selecting the clusters to test.

feat

Integer selecting the feature to test.

indpt

Boolean. If TRUE, assume independent features, otherwise not.

sig

Optional scalar specifying \(\sigma\), relevant if ind is TRUE.

covMat

Optional matrix specifying \(\Sigma\), relevant if ind is FALSE.

Value

stat

the test statistic: the absolute difference between the mean of feature feat in cluster k1 and the mean of feature feat in cluster k2

pval

the p-value

trunc

object of the type Intervals containing the conditioning set

Details

In order to account for the fact that the clusters have been estimated from the data, the p-values are computed conditional on the fact that those clusters were estimated. This function computes p-values exactly via an analytic characterization of the conditioning set.

Currently, this function supports squared Euclidean distance as a measure of dissimilarity between observations, and the following six linkages: single, average, centroid, Ward, McQuitty (also known as WPGMA), and median (also kown as WPGMC).

By default, this function assumes that the features are independent. If known, the variance of feature feat (\(\sigma\)) can be passed in using the sigma argument; otherwise, an estimate of \(\sigma\) will be used.

Setting ind to FALSE allows the features to be dependent, i.e. \(Cov(X_i) = \Sigma\). If known, \(\Sigma\) can be passed in using the covMat argument; otherwise, an estimate of \(\Sigma\) will be used.

References

Yiqun T. Chen and Lucy L. Gao "Testing for a difference in means of a single feature after clustering". arXiv preprint (2023).

See also

rect_hier_clusters for visualizing clusters k1 and k2 in the dendrogram;

Examples

# Simulates a 100 x 2 data set with three clusters
set.seed(123)
library(CADET)
dat <- rbind(c(-1, 0), c(0, sqrt(3)), c(1, 0))[rep(1:3, length=100), ] +
matrix(0.2*rnorm(200), 100, 2)

# Average linkage hierarchical clustering
hcl <- hclust(dist(dat, method="euclidean")^2, method="average")

# plot dendrograms with the 1st and 2nd clusters (cut at the third split)
# displayed in blue and orange
plot(hcl)
rect_hier_clusters(hcl, k=3, which=1:2, border=c("blue", "orange"))


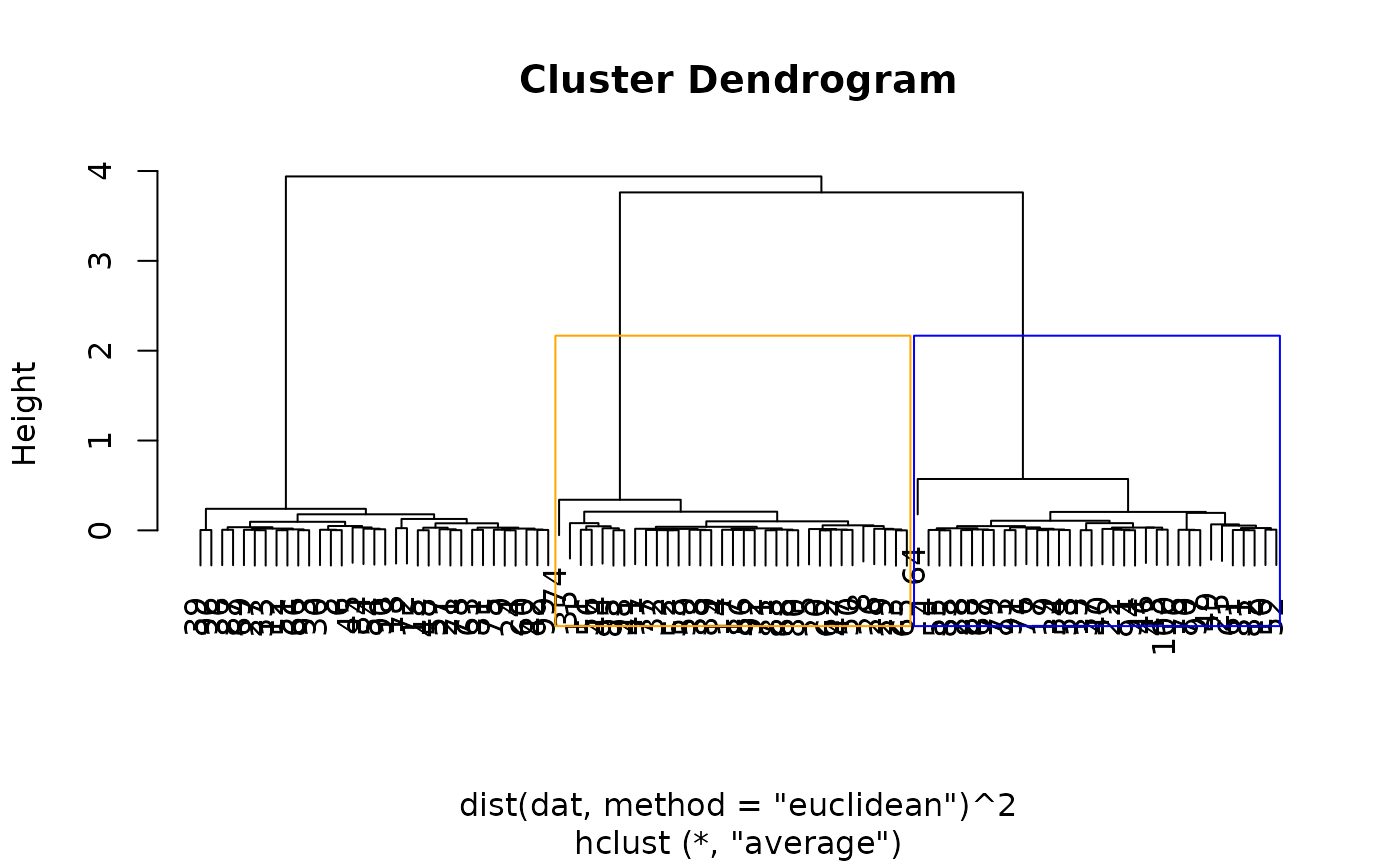# tests for a difference in means between the blue and orange clusters
# with respect to the 1st feature
test_hier_clusters_exact_1f(X=dat, link="average", hcl=hcl, K=3, k1=1, k2=2, feat=1)
#> $stat
#> [1] -0.9469145
#> 
#> $cluster_1
#> [1] 1
#> 
#> $cluster_2
#> [1] 2
#> 
#> $pval
#> [1] 1.001053e-06
#> 
#> $p_naive
#> [1] 2.002035e-06
#> 
#> $trunc
#> Object of class Intervals
#> 2 intervals over R:
#> (-Inf, 0.791767114050557)
#> (4.48600166611002, Inf)
#> 
#> $linkage
#> [1] "average"
#> 
#> attr(,"class")
#> [1] "hier_inference"